ShaZam深入分析之从数字声音到频率

我们在之前的文章中介绍了如何从模拟声音转变到数字声音。现在假如有了一个数字声音，你如何得到他的频率呢？这个部分很重要，因为ShaZam的算法基本都是基于频率的。

对模拟信号来说，这里有一个变化称为连续傅里叶变换。它可以把一个时间的函数转变成频率的函数。也就是假如把傅里叶变换应用到一个声音上，你就会得到它的频率。

但是这里有两个问题：

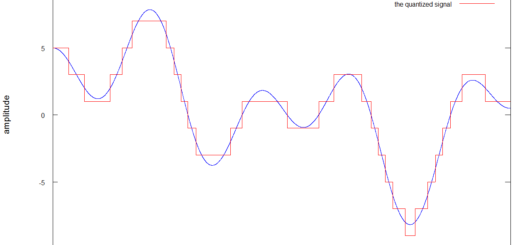
• 我们处理的数字信号，所以它是一个有限的不连续声音。
• 为了更好地理解音乐内部的频率，我们需要把傅里叶变换应用到整个音乐信号的更好的部分，比如我们需要把它应用到0.1s的部分。

还好，我们这里有一个新的数学函数，称之为离散傅里叶变换。

离散傅里叶变换

DFT(离散傅里叶变换）应用到离散信号中，并且返回一个离散的光谱。下面这里是它的公式：

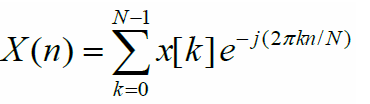
这个公式中：

• N是窗口的大小：组成信号的样本数目
• X(n)代表第n个频率区间
• x(k)是音频信号中的第k个样本

例如，对一个有4096个样本的音频信号，我们需要应用这个公式4096次：

• n=0计算第0个频率区间
• n=1计算第一个频率区间
• n=2计算第二频率区间

你也许注意到，我说的是频率区间而不是频率。这是因为DFT给出的离散光谱。频率区间是DFT能够计算的最小频率单元。频率区间的大小等于信号的采样率除以窗口的大小（N)。在我们上面的例子中，有4096个窗口，标准的声音采样率是44.1kHz，所以频率分辨率就是10.77Hz （第0个有点特殊）

• 第0个频率区间是0Hz到5.38Hz
• 第一个频率区间是5.38Hz到16.15Hz
• 第二个频率区间是16.15Hz到26.92Hz
• 第三个频率区间是26.92Hz到37.68Hz

这就意味着DFT不能够区分小于10.77Hz的两个频率。比如27Hz，32Hz，37Hz其实都落在同一个频谱区间。假如37Hz的音符比较重，你只会知道第三个频率区间比较重。这个对最低八度音阶的解离其实是有问题的，比如：

• A1在55Hz，而B1在58.27Hz以及G1在49Hz。
• 标准88键的第一个音符实在A0 27.5Hz，然后后面是A#0位于29.14Hz

你可以通过增加窗口大小来改进频率分辨率，但这也意味着会丢失音乐中的快速频率/音符的改变：

一个音乐信号的采样率是44.1 kHz

• 增加窗口的大小意味着增加更多的样本，因此就是增加window的时间。
• 对于4096样本，这个window的时间就是0.1秒，频率分辨率是10.7Hz：你可以每0.1s探测一次改变
• 对于16384样本，这个window的时间就是0.37s，频率分辨率就是2.7Hz：你只能探测到0.37s的改变。

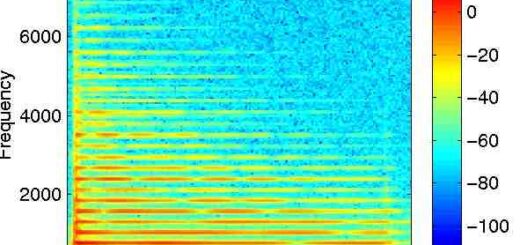
音频信号的一个特殊性就是只需要通过DFT计算一般的频率区间。在之前的定义中，频率区间的定义是10.7Hz，这也就意味着2047个的频率区间展现了从21902.9Hz到21913.6Hz。但是：

• 第2048个频率区间和第0个是一样的
• 第2049个频率区间和第一个也是一样的
• X+2048和第X个是一样的

参考文章：http://coding-geek.com/how-shazam-works/