SHA-2是如何工作的:一个关于SHA-256的教程
SHA-2 (安全散列算法2),其中包括SHA-256,是一个非常流行的散列算法。本文,我们将通过一个实例来尽可能地把这个算法简单的介绍一下。
SHA-2以他的安全性著称,(不像SHA-1那样容易破解),并且它的速度很快。在未生成密钥的情况下,比如挖掘比特币,像SHA-2这种快速的hash算法是非常有优势的。
什么是一个哈希函数?
假如你想比较详细的立即通用的哈希函数,可以参考这里。本文就不详细介绍了,不过我们还是要回顾一下哈希函数的三个重要的作用:
- 确定性的加扰数据。
- 接收任何长度的输入,但是输入的长度是固定的。
- 操作不可逆,也就是说不能从输出推出输入。
SHA-2 VS SHA-256
SHA-2是一个算法,他是一个通用的产生hash数据的想法。SHA-256就是假如一些额外的常量,用来定义SHA-2算法的行为。一个比较常见的常量就是输出的长度。比如256或者512,用这个来设置他们输出的比特大小。
下面让我们来一步一步看一个关于SHA-256的例子。
SHA-256 “Hello World”
第一步 – 预处理
- 把“hello world”转变为二进制:

- 在后面加上一个1

- 填充0,使得它是512的整数倍减去64比特,我们这里选择了448比特
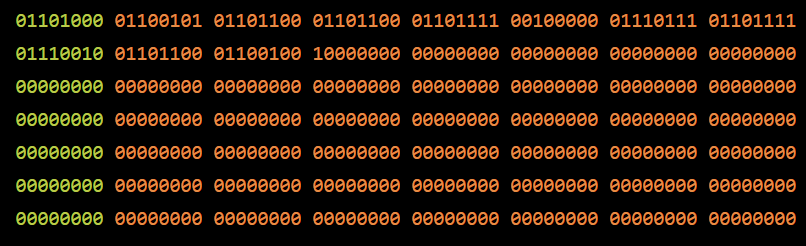
- 在最后加入64比特,这个64比特用来表示之前输入的二进制的长度,用大端来表示。我们这里是88,所以二进制就是“1011000”
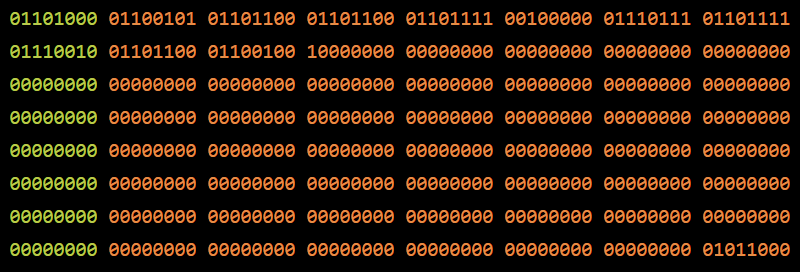
这样我们就有了我们的输入,他总是可以被512整除的。
第二步 — 初始化哈希值 (h)
现在我们来创建8个哈希值,他们是硬编码,代表前8个素数的平方根的小数部分的前32位: 2,3,5,7,11,13,17,19

第三步 — 初始化一个舍入常数 (k)
和第二步类似,我们要创建一个常数 (关于这些常数更多信息以及什么时候使用他们可以参见这里)。这篇文章中,我们用到了64个。每个值(0-63)是前64个素数(2-311)的立方根小数部分的前32位。

第四步 — 块循环
下面这些步骤每512比特(一块)循环一次。在我们的例子中,因为“hello world”比较短,我们只有一个块。在循环的每一个迭代中,我们都需要对哈希值得h0-h7进行突变,从而产生最终的输出。
第五步 — 创建消息时间表 (w)
- 把上面第一步中的输入数据拷贝到一个新的数组中,每一个元素是一个32比特的word:(我们例子中512就是16个元素)

- 然后增加48个word初始化为0,这样我们就有一个数组w[0…63]

使用下面的算法来修改我们后面假如的全0的元素:
对w[16…63]中的每一个i:
- S0 = (w[i-15]向右旋转7) xor (w[0-15] 向右旋转 18) xor (w[i-15] 右移3)
- S0 = (w[i-2]向右旋转17) xor (w[0-2] 向右旋转 19) xor (w[i-2] 右移10)
- w[i] = w[i-16] + s0 + w[i-7] + s1
我们下面以w[16]为例来详细说明一下:

这样,我们的w中就有64个words了:

第六步 — 压缩
初始化变量a,b,c,d,e,f,g,h让他们的值分别等于我们前面设置的哈希值 h0, h1, h2, h3, h4,h5, h6, h7。
运行下面的压缩循环。这个压缩循环需要突变a .. h的值,如下所示:
i从0到63:
- S1 = (e 向右旋转6) xor (e 向右旋转 11) xor (e 向右旋转 25)
- ch = (e and f) xor ((not e) and g)
- emp1 = h + S1 + ch + k[i] + w[i]
- S0 = (a 向右旋转2) xor (a 向右旋转13) xor (a 向右旋转22)
- maj = (a and b) xor (a and c) xor (b and c)
- temp2 := S0 + maj
- h = g
- g = f
- e = d + temp1
- d = c
- c = b
- b = a
- a = temp1 + temp2
我们来过一下第一个迭代,所有的加法都对2^32取模



这个计算过程要继续做63次,始终改变a-h的值,我们不一一计算了,不过我们最终会有这样的结果:
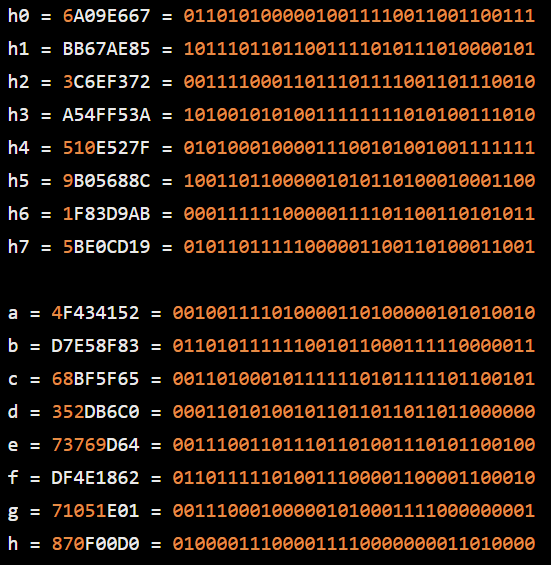
第七步 — 修改最终的值
在压缩循环之后,在每一个块循环内,我们通过加上相应的变量来改变哈希值 a-h。同样的,没有给加法最后都对2^23取模。
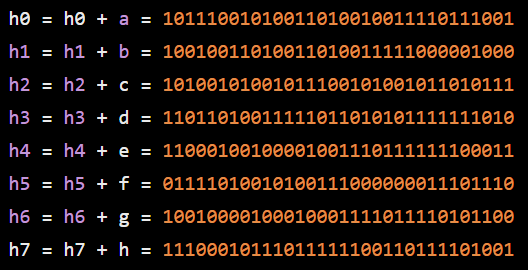
第八步 — 级联最终的哈希值
最后一步,把他们连起来:

好了,这样我们就经历了SHA-256的每一步了。
伪代码
假如你想得到上面所有步骤的伪代码,我们从维基百科得到如下:
![Note
Note
Note
Note
1:
2:
3:
and
the
All
variables are
32 bit
each round, there is
For
The
compression function
Big-endian convention is
unsigned
integers and
addition is calculated
one round constant k[i]
and one entry in the
8 working variables, a through h
uses
modulo 232
message schedule array w[i]
ø
< 1 < 63
used when expressing the constants
in this pseudocode,
when
block data from bytes to words, for example,
parsing message
first word of the input message "abc" after padding is ØX6162638Ø
Initialize hash values:
(first 32 bits of the fractional parts
of the square roots of the first 8 primes 2.
19):
he :
h2 :
h3 .
h4
h5
Ox6aØ9e667
Oxbb67ae85
Ox3c6ef372
Oxa54ff53a
ox51ee527f
ox9b05688c
Oxl f83d9ab
Ox5beøcd19
Initialize array of round constants:
(first 32 bits of the fractional parts
of the cube
exe9b5dba5,
ex55øc7dc3,
ex24Øca1cc,
exbf597fc7 ,
ex53380d13,
exc76c51a3,
ex34bebcb5 ,
ex8cc702Ø8,
2..311):
roots of
the first 64
p r Imes
k[ø. .63]
Ox428a2f98,
Oxd8Ø7aa98,
øxe49b69c1,
Ox983e5152,
Ox27b7øa85,
Øxa2bfe8a1,
Øx19a4c116,
Øx748f82ee,
ex71374491,
exi2835bø1,
exefbe4786,
exa831c66d,
ex2e1b2138,
exa81a664b,
exie376ce8,
ex78a5636f,
Oxb5cøfbc f ,
øx243185be,
Oxefc19dc6,
oxbe0327c8,
øx4d2c6dfc ,
oxc24b8b7e,
øx2748774c,
øx84c87814,
ox3956c25b,
ox72be5d74,
Ox2de92c6f ,
Oxc6eoøbf3,
Ox65Øa7354,
oxd192e819,
ox391cøcb3,
Ox9ebefff a ,
øx59f111f1,
øx8ødeb1f e,
Øx4a7484aa,
Øxd5a79147,
øx766aeabb,
øxd6990624,
Øx4ed8aa4a ,
Øxa45Ø6ceb,
Ox923f82a4,
Ox9bdcø6a7 ,
Ox5 cbøa9dc ,
OxØ6ca6351,
Ox81c2c92e,
oxf4ee3585,
Ox5b9cca4f ,
Oxbef9a3f7 ,
øxabl c5ed5 ,
øxc19bf174,
øx76f988da,
øx14292967 ,
øx92722c85,
Øx1Ø6aaØ7Ø,
øx682e6ff3 ,
øxc67178f2](http://donggeitnote.com/wp-content/uploads/2020/07/image-29-1024x734.png)
![Pre-processing (padding) :
begin with
the original message
of length
append a single '1' bit
append K 'e' bits, where K is the minimum
b:
L bits
number
such that L + 1
64 is
a multiple
of 512
ø
total post-processed length a multiple of 512 bits
append L as a
64-bit big-endian integer,
making the
Process the message in successive 512-bit chunks:
break message into 512 bit chunks
for
each chunk
-entry message schedule
array w[ø. .63] of 32-bit words
create a 64
(The initial values
in w[e. .63] don't matter, so many implementations zero them here
copy chunk into first
words
16
Extend the first 16
words into
i from 16 to 63
.15] of the message schedule
so
sl .
(w[i-15
] rightrotate
(w[i-
2] rightrotate
w[i-16] + sø + w[i-
the
7)
17)
remaining
(w[i-15]
xor
xor
words w[16
rightrotate
rightrotate
.63]
18)
19)
array
of the message schedule
array :
(w[i-15] rightshift 3)
xo r
(w[i- 2] rightshift 10)
xo r
7] + sl
Initialize working variables
to current hash value:
he
h2
h3
ha
h5
h6](http://donggeitnote.com/wp-content/uploads/2020/07/image-30-1024x743.png)

原文地址:https://hackernoon.com/how-sha-2-works-a-step-by-step-tutorial-sha-256-46103t6k

Recent Comments