深入分析数据库中数据的存储和读取

我们日常的开发或多或少都会和数据库打交道，那么数据库中数据都是如何存储来保证读写的效率呢？本文就来详细地介绍数据库中数据的存储和读写。

最简单的数据库

我们首先来看一个最简单的通过bash来实现的数据库，它就是一个键值数据库，通过Bash函数来实现读写。

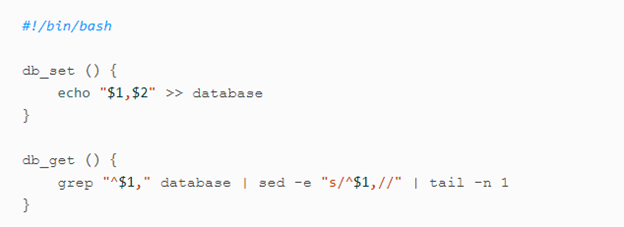
这里有两个函数，一个是写函数，就是简单的写入key和value对。另外一个函数是db_get()函数，它可以读出最新写入的一行数据。

我们可以这样使用它，这里我们就是写入了两个key，value，一个是123456，对应的后面的Json格式数据：'{“name”:”San Francisco”,”attractions”:[“Exploratorium”]}’，另外一个键值是42，它对应的是'{“name”:”San Francisco”,”attractions”:[“Golden Gate Bridge”]}’，最后我们可以调用get函数得到42对应的值。这个实现算是简单明了，一目了然了。

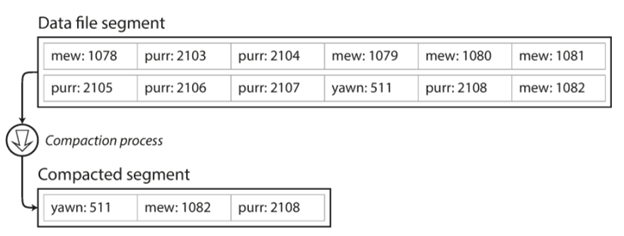
那么假如一个键值被设置了多次该怎么保存了，如下图所示：

我们可以看到，42被重写了，这里最简单的实现就是继续往后面加一行，然后在读取的时候从后往前读（后面就是最新的），就可以得到最新的值了。

其实在真正的数据库中，也有类似的实现就是一个不断增加的log文件，我们会不停地往里面写，当然真实的数据考虑的问题会复杂很多，比如写到一半出问题了，或者写出问题了等等。但是总得思想还是类似的。

聪明的你也许会问，假如我要删除一个key怎么办呢？一般来说，对于删除的操作，我们需要插入一个特殊记录在最后，当我们遍历到这个记录的时候，我们就知道，这个key是被删除了。

当然这种实现的另一个问题就是，随着我们不停地写这个文件的大小是不断增加的，哪怕我们是更新一个同样的key，这个文件也是在不断增大，它最终会带来文件大小的问题。对于这个问题的一般解决方法就是做merge的操作，也就是保存最新的记录即可，这个操作在我们key的值比较少的情况下可以大大缩小文件的大小。

当然还有一个问题也许你会比较好奇，为什么要一直重复往最后加，而不是去更新呢？这是一个很好的问题，有这样几个原因：

1. 一直往后面加，其实可以充分利用到HDD的sequential写，假如你对HDD的读写有研究，你就会知道，sequential写的速度和效率要比随机写高很多，这个主要的原因就是磁盘的磁头不需要随机地不停进行改变。即使是SSD，sequential写相对于随机写也会延长SSD的寿命。
2. 并发和crash的恢复会简单很多。你不需要太担心写到一半发生crash的情况。基本只要做好checksum，就可以知道最后有多少log可能是不对的，去除即可，而不用担心某一个地方更新只更新了一半的情况。

这样的实现其实写的效率还是不错的，因为你只要负责在文件最后不停地写就可以了，但是当数据大了之后，读就会成为问题，你找一个key的值，需要从后往前不停地遍历，也就是o(n)的复杂度了，那么有没有什么好的办法来加快这个进程呢？答案显然是有的，这就是我们下面要讨论的哈希索引。

哈希索引

还是以上面的数据库来作为例子，我们知道文件其实存在磁盘上，它是有一个offset的。假如我们能够有一个in-memory的hash表来保存key和offset的对对应关系，那么读的效率显然会提高很多，如下图所示：

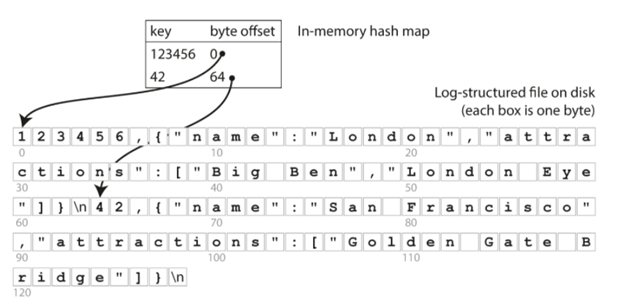
有了这个哈希表，我们就可以知道42对应的位置在64 offset，然后就很容易读到对应的内容，而不需要从后往前遍历。这里的哈希索引有一个问题，就是它其实是in-memory的，也就是说假如发生crash，我们得要重新建立它，这就需要重新遍历这个disk来得到所需要的索引，一个比较好的方法就是我们在disk也保存一份哈希索引的备份，这样出了问题，我们也可以快速恢复。

初一听起来这样的哈希索引还是不错，但是细想一下就会发现其实它也有很多问题：

1. 假如key的数目很多，也就意味着我们需要保存到哈希索引中的内容也很多。
2. 范围的查找效率很低，比如说找key001到key002之间的值，就需要遍历所有的key才能找到相应的答案。

那么如何来解决这些问题呢？我们来看看SSTable和LSM-Tree。

SSTable

我们发现上面介绍的数据库实现中，每一行都是一个key value的对，其实不同key之间的顺序并不重要。也就是说在数据库中，key=42的记录在前面还是key=53的记录在前并不影响最终的结果。这样一来，我们可以在merge的时候，按照key的顺序来排序，我们称这种方法为Sorted String Table简称SSTable。

它的实现也很简单，流程如下：

1. 当有写到来，首先写到一个in-memory的平衡树结构中（比如红黑树），这样开始写到memory而不是disk的原因是一般来说，维护一个有序的memory的结构相比维护一个有序的disk文件要方便很多，我们称这个为memtable。
2. 当memtable越来越大，比如说大于一定的阈值，就会写到磁盘中，因为memtable本身是有序的，所以有序地写到磁盘中就相对比较容易了，我们称每次的写入为一个segment。
3. 假如这个时候有读的操作，那就先访问memtable，然后在一次访问各个segment（从最新到最旧）
4. 后台我们再启动一个线程来merge各个segment，如下图所示：

这样实现之后，我们的index甚至不需要写入所有的key，直接写一个范围即可，如下图所示，假如你想找handful，虽然在index中没有这个key，但是你知道它是位于handbag和handsome之间的，所以只要从handbag的offset开始遍历，找到handsome的offset为止，如果有就返回，只有这个范围设置合理，那么这个小范围的遍历效率还是很高的。这样的index就是我们俗称的Log-Structured Merge-Tree （LSM-Tree）。

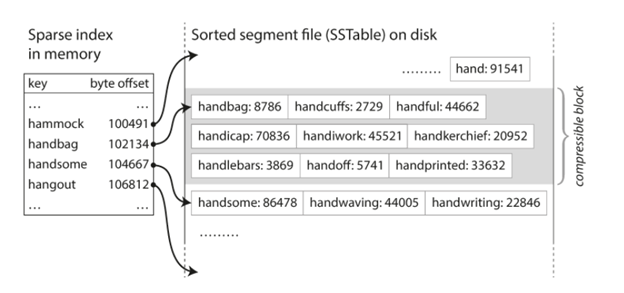
当然LSM-Tree也有一些可以优化的空间，比如说查找不存在的key的效率比较低，你需要先找memtable，再找各个index。一个比较常见的优化就是在内存中维护一个结构，这个结构可以判断一个key是否存在，假如不存在就不需要再去遍历了。另外一个值得研究的领域就是后台的merge操作在什么时间和什么顺序来做比较合理，总得来说有两大类方法，一种就是把小的新的segment合并到大得新的segment。另外一种方法就是按照key的范围来做merge。

B-Tree

我们上文提到的LSM-Tree很不错，但是它在现实中并不是使用最广泛的，我们通常会使用B-Tree。

B-Tree和LSM-Tree唯一比较类似的地方就是他也是把key进行按序排列的。LSM-Tree是把数据分成不同大小的segment，而B-Tree则不同，它会把数据库分成固定大小的块或者页，一般来说是4KB，每次读写都是一页。这种设计和磁盘的设计是类似的。

如下图所示，每一页都是通过一个地址来区分，这样就可以从一页指向另外一页，就像指针一样。就是类似一个层级的结构，比如我们要找251，首先找到它所在的区间200到300，然后在下一个层级中再找到它所在的区间250到270，再往下一层就可以找到251了。

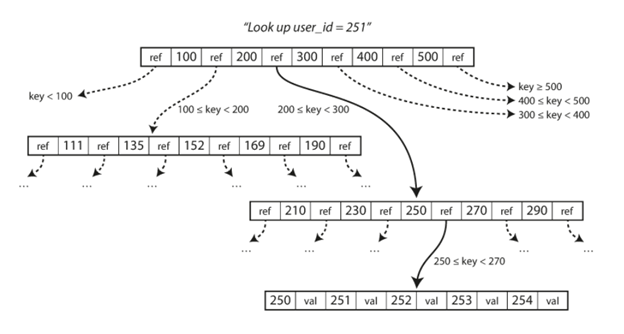
这里每一个层级所指向的页面的数目我们称之为Branching factor，在我们的例子中它就是6。现实的例子基本有数据大小来决定的，基本上是几百的量级。最终保存数据的最后一层页面我们称之为叶子页（leaf page）。

假如我们需要更新值很简单，只要找到对应的值，更新即可，其它部分可以保持不变。但是假如我们需要插入一个值，就有可能有问题，比如它的数据超过了我们页面的大小，就需要把页面分成两个页面了，如下图所示：

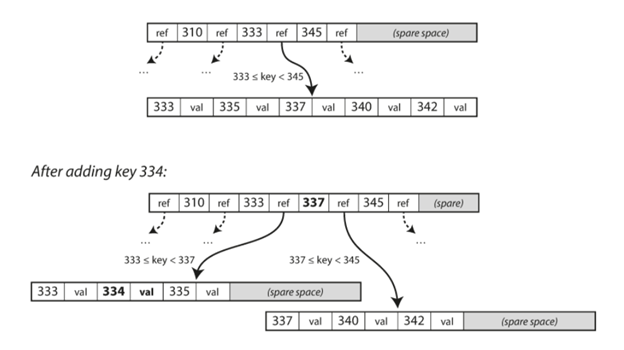
这样的算法基本可以满足目前大部分的数据库的要求，比如我们把branching factor设为500，每一个页面是4KB，有4层的树，我们可以保存256TB的数据。

这样的结构会有一个问题，就是我们每次写的是一个页面，而这个过程就会有一个问题，那就是写了一半crash了，假如这种问题发生，我们就会只有一半的数据。所以通常来说我们还会保存一个不停往前写的log文件，这个log文件会在我们真正更新B-Tree之前更新，这样假如我们在更新B-Tree的过程中发生问题，我们还可以从这个log文件中恢复数据。

当然除了这种方法来防止crash之外，还有很多别的方法，比如会同时维护两份页面，当新的页面更新成功之后，就直接修改指针指过去就好。

当然B-Tree已经有一段时间了，很多人都做了很多的优化，比如会尝试把每个页面在磁盘中的存储位置也尽量按序排列，这样在读的时候就会是一个sequential的访问，提高访问的效率。又比如可以在每一个叶子页面加一个向前和向后的指针指向前后排序的页面，这样我们查询一个范围的时候效率就会更高等等。