ShaZam深入分析之音乐基础
我们都知道声音是通过空气(或水等介质)进行传播的振动,然后由人的耳朵进行解析的。比如我们听音乐,声音就是通过空气传播,然后被你的耳朵所接受。光也和声音类似,只是说这次你的耳朵没法解析它,但是你的眼睛可以。本文就来介绍一下,音乐是如何用物理、技术进行描述的。
纯音和真实的声音
所谓的纯音就是正弦波形的音。正弦波有下面这些特性:
- 它的频率: 每秒的循环数,它的单位是赫兹(HZ),比如100Hz = 100循环/s
- 它的振幅(声音的大小相关):每一个循环的大小
人耳就是通过解析这些特性来组成声音的。人耳可以听到20 Hz 到 20000Hz的声音,而随着岁数的增加,这个范围不断地在缩小。
人耳对响度的感知取决于纯音的频率,比如一个30Hz的(振幅10)纯音听起来比100Hz(振幅10)的要轻。人耳遵循心理声学模型,具体你可以参考这边文章。

上图显示的就是一个纯音的波形,它的频率是20Hz,振幅是1.
纯音在自然界并不存在,但是任何声音其实都可以看成是多个不同振幅纯音的组合。

上面这幅图,你可以看成它是由多个正弦波组成的:
- 一个20Hz,振幅1的正弦波
- 一个40Hz,振幅2的正弦波
- 一个80Hz,振幅1.5的正弦波
- 一个160Hz,振幅1的正弦波。
现实世界中的声音可能由成百上千个纯音组成。
音符

音乐其实是由一系列音符组成的,这些音符也有长短和大小。
音符可以分成八度,也就是我们常说的A,B,C,D,E,F,G或者Do,Re,Mi,Fa,Sol,La,Si。而且它们有下面这些特性:
- 音符的频率是上一个八度的两倍,比如说A4的(A在第四度)的频率是440Hz,它就是A3的频率(220Hz)的两倍,是A2(110Hz)的四倍。
很多乐器以八度为单位提供了高于八个音符,我们称之为半音。

对第四度音来说,这些音符的频率如下:
- C4(Do3) = 261.63Hz
- D4(Re3) = 293.67Hz
- E4(Mi2) = 329.63HZ
- F4 (or Fa3) = 349.23Hz
- G4 (or Sol3) = 392Hz
- A4 (or La3) = 440Hz
- B4 (or Si3) = 493.88Hz
虽然它们是奇数,但是人耳的敏感度其实是对数的,也就意味着在区间32.70Hz到61.74Hz (第一度),以及261.63Hz和466.16Hz(第四度),或者2093Hz和3951.07Hz(第七度),人耳检测到的音符是一样的。
音色
同样的音符假如由不同的乐器发出,比如吉他,钢琴,或者人唱歌,听起来是完全不一样的。这是因为他们的音色不同。对于每种乐器,产生的声音就像是给定音符的不同频率(也就是专业上说的音高)。声音有一个基础的频率(最低的频率)以及多个范音(高于基频的频率)。
很多乐器产生(或接近)和声,对这些乐器来说,泛音是基频的倍数,称之为和声。
频谱图
一个音乐会由多个乐器和歌手共同完成。所有这些乐器都产生多个不同频率的正弦波从而组合一个新的正弦波。
我们可以用频谱图来分析音乐,很多时候,频谱图是由一个三维图来表示的:
- 横轴X表示时间。
- 纵轴y表示纯音的频率
- 第三维是由颜色来表示的,它表示了某个时间点,某个频率的振幅。
比如下面就是一个频谱图(C4音符,钢琴弹奏)。
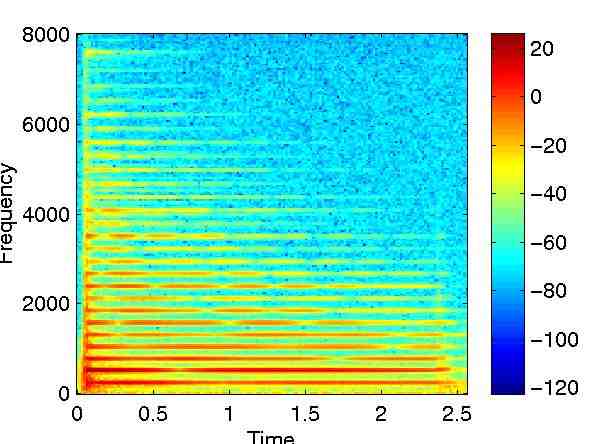
就像我们上面提到的,虽然它是C4的音符,但是这里有别的频率(而不是仅仅261Hz),也就是泛音。有趣的是,别的频率都是第一个的倍数。另一个有趣的事是频率的强度会随着时间变化,这就是不同乐器之间进行区分的所在。假如你不是用钢琴进行弹奏,那么这个地方就有稍许不同。从技术上来讲,频率的这些变化正在改变声音信号的包络。
这里就有了Shazam的音乐指纹算法第一个思想:频谱上一些频率是比别的频率更重要的(最低的频率)。
好了,第一部分音乐的机理就给大家讲到这里了,我们下一篇再见。

Recent Comments